A team of physicists has uncovered a hidden topological structure within one of the most widely used sources of quantum entanglement.



Over the past decades, energy engineers have developed increasingly advanced battery technologies that can store more energy, charge faster and maintain their performance for longer. In recent years, some researchers have also started exploring the potential of quantum batteries, devices that can store energy leveraging quantum mechanical effects.
To store energy, quantum batteries rely on qubits, quantum systems that can exist in two energy states simultaneously, leveraging a property known as superposition. While in principle these batteries could perform better than classical batteries, the realization of battery prototypes that exhibit this predicted quantum advantage has proved challenging.
Researchers at the Southern University and Technology in China (Sustech) and the Superior Council for Scientific Research (CSIC) in Spain recently realized a quantum energy storage device that was found to outperform a classical equivalent when operating under realistic conditions.

Researchers at the Harvard John A. Paulson School of Engineering and Applied Sciences (SEAS) have created a chip-scale device that can dynamically control the “handedness” of light as it passes through—also known as its optical chirality—with a simple twist of two specially designed photonic crystals. The study is published in the journal Optica.
The work, led by graduate student Fan Du in the lab of Eric Mazur, the Balkanski Professor of Physics and Applied Physics, describes a reconfigurable twisted bilayer photonic crystal that can be tuned in real time using an integrated micro-electromechanical system (MEMS). The breakthrough opens new possibilities for advanced chiral sensing, optical communication, and quantum photonics.
“Chirality is very important in many fields of science—from pharma to chemistry, biology, and of course, physics and photonics,” Mazur said. “By integrating twisted photonic crystals with MEMS, we have a platform that is not only powerful from a physics standpoint, but also compatible with the way modern photonics are manufactured.”

Photonic chips use light to process data instead of electricity, enabling faster communication speeds and greater bandwidth. Most of that light typically stays on the chip, trapped in optical wires, and is difficult to transmit to the outside world in an efficient manner.
If a lot of light could be rapidly and precisely beamed off the chip, free from the confines of the wiring, it could open the door to higher-resolution displays, smaller Lidar systems, more precise 3D printers, or larger-scale quantum computers.
Now, researchers from MIT and elsewhere have developed a new class of photonic devices that enable the precise broadcasting of light from the chip into free space in a scalable way.

An international research team led by Alexander Kuznetsov at the Paul Drude Institute for Solid State Electronics (PDI) in Berlin has demonstrated a fundamentally new way to control the condensation of hybrid light-matter particles. Using coherent acoustic driving to dynamically reshape the energy landscape of a semiconductor microcavity, the researchers achieved deterministic steering of a macroscopic quantum state into its lowest energy configuration.
The results, published in Nature Photonics, establish a strategy for engineering nonequilibrium quantum states and open prospects for ultrafast, tunable photonic technologies.
In collaboration with long-term partners from the National Scientific and Technical Research Council CONICET and the Bariloche Atomic Center and Balseiro Institute in Argentina, the team experimentally realized a universal scheme for selectively transferring populations within a multilevel quantum system using strong time periodic modulation.

Ultrashort mid-infrared (mid-IR) laser pulses are essential for applications such as molecular spectroscopy, nonlinear microscopy, and biomedical imaging, but their generation often relies on complex and power-intensive systems that are difficult to implement outside of specialized laboratories. These systems usually require high pump powers, elaborate optical setups, and precise alignment, which can limit their widespread adoption and practical use in everyday research and clinical settings.
In a paper published in the IEEE Journal of Quantum Electronics, a team of researchers from SASTRA Deemed University, Thanjavur, report a compact, fiber-based method for generating clean ultrashort mid-IR pulses at significantly reduced input power.
The study demonstrates that high-quality pulse compression can be achieved using a holmium-doped ZBLAN photonic crystal fiber integrated into a nonlinear optical loop mirror (NOLM), offering a simpler and more energy-efficient alternative to conventional systems.
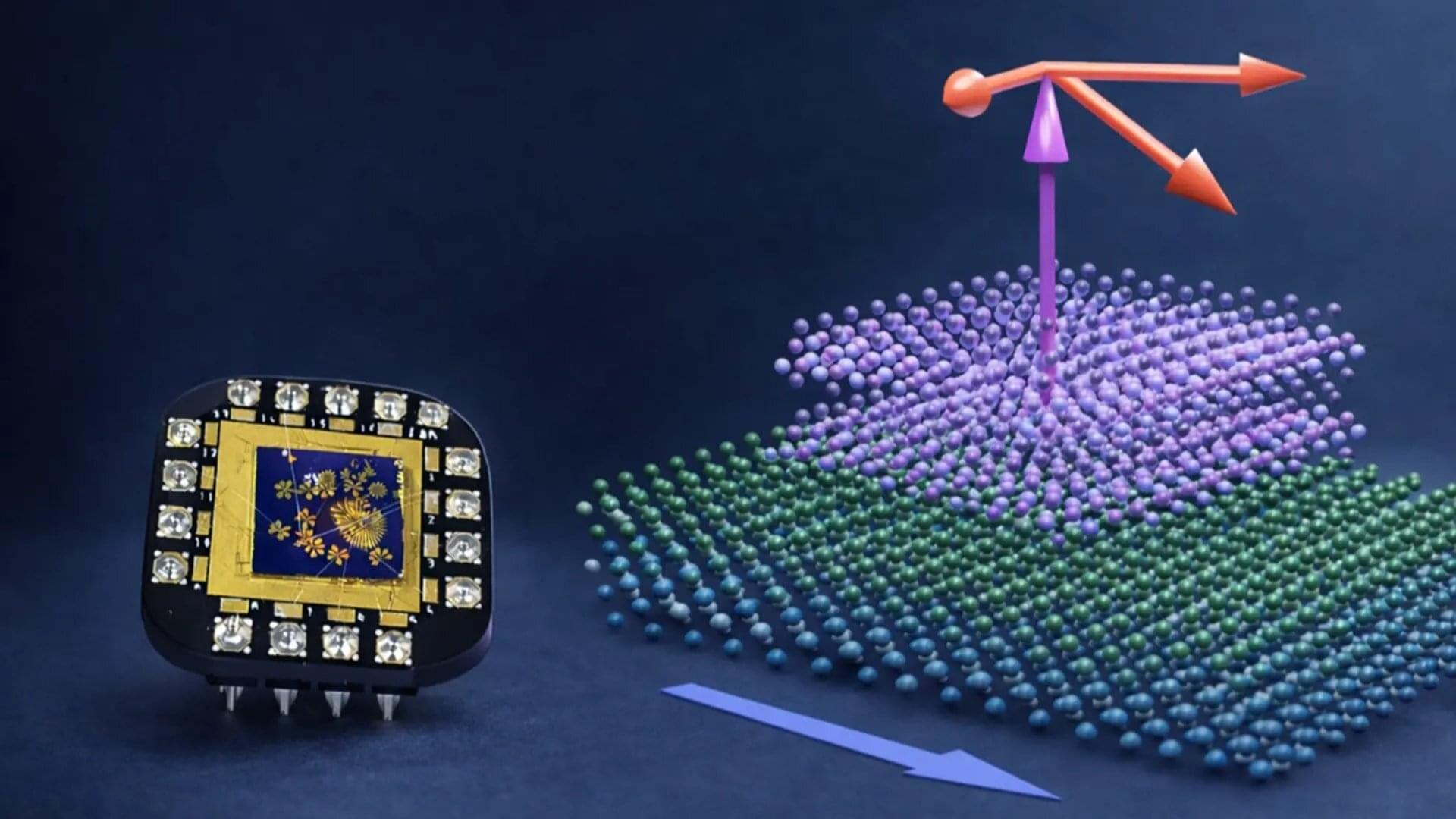
Spintronics—a technology that harnesses the electron’s magnetic quantum states to carry information—could pave the way for a new generation of ultra-energy-efficient electronics. Yet a major challenge has been the ability to control these delicate quantum properties with sufficient precision for practical applications. By combining different quantum materials, researchers at Chalmers University of Technology have now taken a decisive step forward, achieving unprecedented control over spin phenomena. The advance opens the door to next-generation low-power data processing and memory technologies.
Data centers, cloud services, AI and connected systems account for a rapidly growing share of global energy consumption. In the quest for new, more energy-efficient technological solutions, spin electronics, or spintronics, has proven to be a new and promising approach. Instead of relying solely on the movement of electric charge, spintronics use magnetic states to carry information. More specifically, it takes advantage of a quantum property of electrons known as spin, which makes electrons behave like tiny magnets.
“Just like a compass needle, an electron’s spin can point in one of two directions—up or down. These two directions can be used to represent digital information, in the same way today’s electronics use 0s and 1s,” explains Saroj Dash, Professor of Quantum Device Physics at Chalmers University of Technology.
Take your scientific understanding to the next level with Brilliant! Start learning for free at https://brilliant.org/sabine/ and get a 30-day free trial plus 20% off a premium subscription, which includes daily unlimited access!
What is space, really? That’s one of the biggest questions in science. According to a pair of researchers from the Perimeter Institute, the answer to that is: a quasicrystal. What is a quasicrystal, and how is space a quasicrystal? Let’s take a look.
Paper: https://arxiv.org/abs/2601.
👕T-shirts, mugs, posters and more: ➜ https://sabines-store.dashery.com/
💌 Support me on Donorbox ➜ https://donorbox.org/swtg.
👉 Transcript with links to references on Patreon ➜ / sabine.
📝 Transcripts and written news on Substack ➜ https://sciencewtg.substack.com/
📩 Free weekly science newsletter ➜ https://sabinehossenfelder.com/newsle… Audio only podcast ➜ https://open.spotify.com/show/0MkNfXl… 🔗 Join this channel to get access to perks ➜ / @sabinehossenfelder 📚 Buy my book ➜ https://amzn.to/3HSAWJW #science #sciencenews #spacetime #physicsteacher What is space? That’s one of the biggest questions, not just in the foundations of physics, but in all of science. According to a new paper, the answer may be a quasicrystal, an idea from researchers working on quantum gravity. This video explores the implications of this idea, touching on concepts like String Theory and Loop Quantum Gravity, to understand what it might mean for theoretical physics.
👂 Audio only podcast ➜ https://open.spotify.com/show/0MkNfXl…
🔗 Join this channel to get access to perks ➜
/ @sabinehossenfelder.
📚 Buy my book ➜ https://amzn.to/3HSAWJW
#science #sciencenews #spacetime #physicsteacher.
What is space? That’s one of the biggest questions, not just in the foundations of physics, but in all of science. According to a new paper, the answer may be a quasicrystal, an idea from researchers working on quantum gravity. This video explores the implications of this idea, touching on concepts like String Theory and Loop Quantum Gravity, to understand what it might mean for theoretical physics.

Electron movement and structures described in quantum physics allow researchers to better understand how and why materials like superconductors behave as they do. Rice University researchers Jianwei Huang and Ming Yi have developed a new capability, magnetoARPES, building on angle-resolved photoemission spectroscopy (ARPES) that allows researchers to study quantum behaviors they have been unable to resolve using ARPES alone. The work has been published in Nature Physics.
MagnetoARPES adds a tunable magnetic field, external to the sample, to ARPES. This allows researchers to probe the full electronic response to a magnetic field, giving insights into why certain collective behaviors of electrons develop.
Magnetic fields have, historically, been excluded from ARPES experiments, but over the course of a few years of experimentation and simulations, Yi’s team found a viable way to incorporate this capability into the ARPES sample environment.

Hydrogen fuel is a promising alternative to fossil fuels that only emits water vapor when used and could thus help to lower greenhouse gas emissions on Earth. In the future, it could potentially be used to fuel heavy-duty transport vehicles, such as trucks, trains, and ships, as well as industrial heating and decentralized power generation systems.
Unfortunately, most current methods to produce hydrogen rely on the burning of fossil fuels, which limits its environmental advantages. Given its potential, many energy engineers worldwide have been trying to devise more sustainable strategies to produce hydrogen on a large scale.
One proposed method for the clean production of hydrogen is known as photocatalytic water splitting. This approach entails splitting water molecules into hydrogen and oxygen, using photocatalysts (i.e., materials that respond to sunlight and prompt desired chemical reactions).