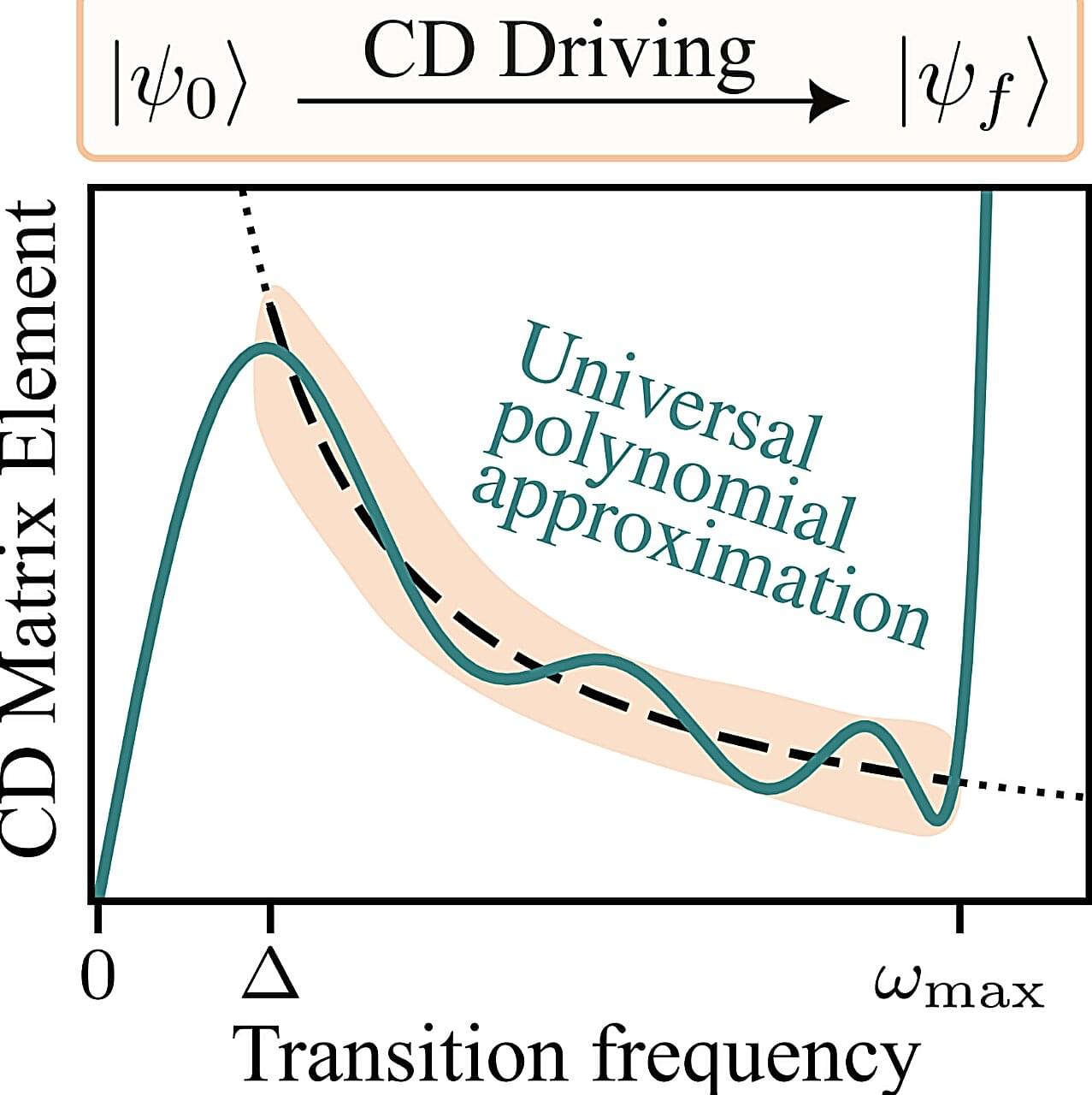
Stephen Wolfram is a physicist, mathematician, and programmer who believes he has discovered the computational rules that organize the universe at the finest grain. These rules are not physical rules like the equations of state or Maxwell’s equations. According to Wolfram, these are rules that govern how the universe evolves and operates at a level at least one step down below the reality that we inhabit. His computational principles are inspired by the results observed in cellular automata systems, which show that it’s possible to take a very simple system, with very simple rules, and end up at complex patterns that often look organic and always look far more intricate than the black and white squares that the game started with. He believes that the hyperspace relationships that emerge when he applies a computational rule over and over again represent the nature of the universe — and that the relationships that emerge contain everything from the seed of human experience to the equations for relativity, evolution, and black holes. We sit down with him for a conversation about the platonic endeavor that he has undertaken, where to draw the line between lived experience and the computational universe, the limits of physics, and the value of purpose and the source of consciousness.
MAKE HISTORY WITH US THIS SUMMER:
https://demystifysci.com/demysticon-2025
PATREON
/ demystifysci.
PARADIGM DRIFT
https://demystifysci.com/paradigm-drift-show.
Material solutions to quantum spookiness: https://www.youtube.com/@MaterialAtomics.
00:00 Go!