George Karniadakis, a professor of applied math and engineering, was one of nine faculty scientists and engineers from across the U.S. to receive a Vannevar Bush Faculty Fellowship.


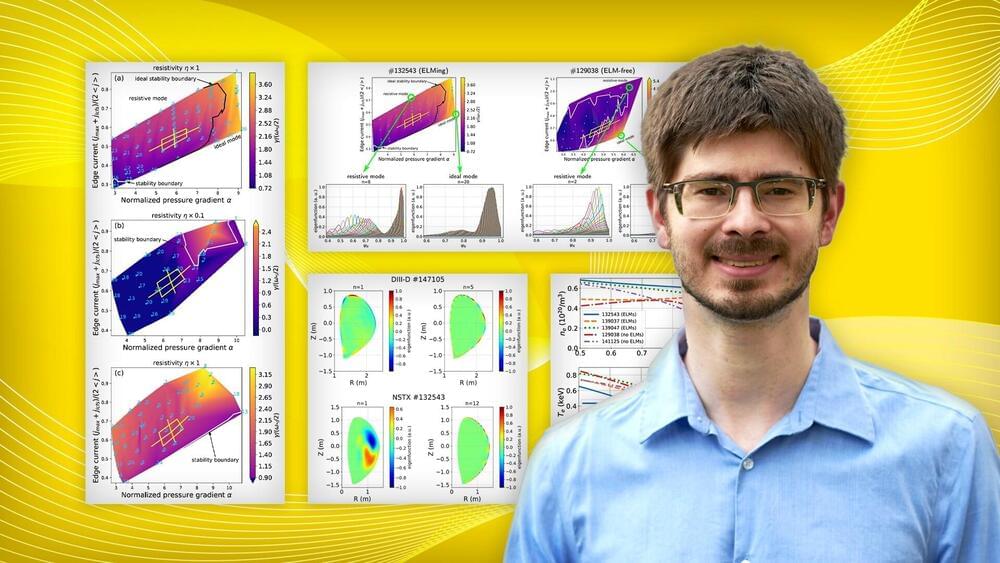
Researchers at the U.S. Department of Energy’s (DOE) Princeton Plasma Physics Laboratory (PPPL) have found that updating a mathematical model to include a physical property known as resistivity could lead to the improved design of doughnut-shaped fusion facilities known as tokamaks.
“Resistivity is the property of any substance that inhibits the flow of electricity,” said PPPL physicist Nathaniel Ferraro, one of the collaborating researchers. “It’s kind of like the viscosity of a fluid, which inhibits things moving through it. For example, a stone will move more slowly through molasses than water, and more slowly through water than through air.”
Scientists have discovered a new way that resistivity can cause instabilities in the plasma edge, where temperatures and pressures rise sharply. By incorporating resistivity into models that predict the behavior of plasma, a soup of electrons and atomic nuclei that makes up 99% of the visible universe, scientists can design systems for future fusion facilities that make the plasma more stable.

The bottomless bucket is Karl Marx’s utopian creed: “From each according to his ability, to each according to his needs.” In this idyllic world, everyone works for the good of society, with the fruits of their labor distributed freely — everyone taking what they need, and only what they need. We know how that worked out. When rewards are unrelated to effort, being a slacker is more appealing than being a worker. With more slackers than workers, not nearly enough is produced to satisfy everyone’s needs. A common joke in the Soviet Union was, “They pretend to pay us, and we pretend to work.”
In addition to helping those who in the great lottery of life have drawn blanks, governments should adopt myriad policies that expand the economic pie, including education, infrastructure, and the enforcement of laws and contracts. Public safety, national defense, dealing with externalities are also important. There are many legitimate government activities and there are inevitably tradeoffs. Governing a country is completely different from playing a simple, rigged distribution game.
I love computers. I use them every day — not just for word processing but for mathematical calculations, statistical analyses, and Monte Carlo simulations that would literally take me several lifetimes to do by hand. Computers have benefited and entertained all of us. However, AI is nowhere near ready to rule the world because computer algorithms do not have the intelligence, wisdom, or commonsense required to make rational decisions.

Research in the field of machine learning and AI, now a key technology in practically every industry and company, is far too voluminous for anyone to read it all. This column, Perceptron, aims to collect some of the most relevant recent discoveries and papers — particularly in, but not limited to, artificial intelligence — and explain why they matter.
In this batch of recent research, Meta open-sourced a language system that it claims is the first capable of translating 200 different languages with “state-of-the-art” results. Not to be outdone, Google detailed a machine learning model, Minerva, that can solve quantitative reasoning problems including mathematical and scientific questions. And Microsoft released a language model, Godel, for generating “realistic” conversations that’s along the lines of Google’s widely publicized Lamda. And then we have some new text-to-image generators with a twist.
Meta’s new model, NLLB-200, is a part of the company’s No Language Left Behind initiative to develop machine-powered translation capabilities for most of the world’s languages. Trained to understand languages such as Kamba (spoken by the Bantu ethnic group) and Lao (the official language of Laos), as well as over 540 African languages not supported well or at all by previous translation systems, NLLB-200 will be used to translate languages on the Facebook News Feed and Instagram in addition to the Wikimedia Foundation’s Content Translation Tool, Meta recently announced.

At the heart of every resonator—be it a cello, a gravitational wave detector, or the antenna in your cell phone—there is a beautiful bit of mathematics that has been heretofore unacknowledged.
Yale physicists Jack Harris and Nicholas Read know this because they started finding knots in their data.
In a new study in the journal Nature, Harris, Read, and their co-authors describe a previously unknown characteristic of resonators. A resonator is any object that vibrates only at a specific set of frequencies. They are ubiquitous in sensors, electronics, musical instruments, and other devices, where they are used to produce, amplify, or detect vibrations at specific frequencies.

Yes, it is true, cats are known to possess certain math skills in their own feline manner. Although it is obvious, they don’t have the knowledge of trigonometry or geometry as we do, but they sure understand the concept of ‘more and less’.
Every cat owner knows they get notified by their cat if the food dish is getting empty or the water is relatively less in the bowl. Furthermore, as they grow, cats can adeptly tell the difference between heights.
Albeit, this is still an ongoing study and researchers have found similarities between the thinking process of fish and that of cats. Fish swim in schools, and that’s how they learn to count. Likewise, adult cats or rather mother cats can identify if one of the kittens is missing.

Everything we know, think and feel—everything!—comes from our brains. But consciousness, our private sense of inner awareness, remains a mystery. Brain activities—spiking of neuronal impulses, sloshing of neurochemicals—are not at all the same thing as sights, sounds, smells, emotions. How on earth can our inner experiences be explained in physical terms?
Free access to Closer to Truth’s library of 5,000 videos: http://bit.ly/376lkKN
Watch more interviews on consciousness and neurology: https://bit.ly/3Re9Xc1
Peter Ulric Tse is Professor of Cognitive Neuroscience in the department of Psychological and Brain Sciences at Dartmouth College. He holds a BA from Dartmouth (1984; majored in Mathematics and Physics), and a PhD in Experimental Psychology from Harvard University (1998).
Register for free at CTT.com for subscriber-only exclusives: http://bit.ly/2GXmFsP
Closer to Truth, hosted by Robert Lawrence Kuhn and directed by Peter Getzels, presents the world’s greatest thinkers exploring humanity’s deepest questions. Discover fundamental issues of existence. Engage new and diverse ways of thinking. Appreciate intense debates. Share your own opinions. Seek your own answers.

Curiosity is important for human development and learning and encourages an exploration for new information. New research published in the Journal of Individual Differences found that high dispositional curiosity is related to greater general knowledge, but not necessarily related to fluid intelligence.
Curiosity is important for both crystallized intelligence (i.e., one’s general knowledge) and fluid intelligence (i.e., one’s ability to reason and use novel information). “Seeking out new environments, being more attentive, and exploring more and more comprehensively might, in turn, also increase the probability of gaining new information,” explain study author Freda-Marie Hartung and colleagues. “Thus, it is plausible to assume that interindividual differences in epistemic curiosity are related to interindividual differences in general knowledge.”
Thus, the researchers were interested in how dispositional curiosity influences one’s acquisition of knowledge and how fluid intelligence affects this relationship. Hartung and her colleagues recruited 100 participants during lectures at a German University to complete a self-report questionnaire on the relevant personality traits (i.e., curiosity, conscientiousness, social anxiety). They also completed measures assessing their general knowledge (i.e., geography, history, math, natural sciences) and fluid intelligence (i.e., reasoning and memory tasks).

While we haven’t found any evidence of alien life yet, that doesn’t mean it’s not out there, beyond our reach. Now, a team of researchers has put together a mathematical model showing aliens could potentially be communicating across space – via quantum physics.
Efforts are well underway to make quantum communications a reality here on Earth. The idea is that quantum mechanics provide certain properties that would make information transfer inherently faster and more secure than regular systems… if we can get it to work.
One of the major hurdles to overcome before quantum networks can be established is that they’re very fragile and susceptible to interference. According to this latest study, such networks could fly across space without breaking up.