Lifeboat Foundation

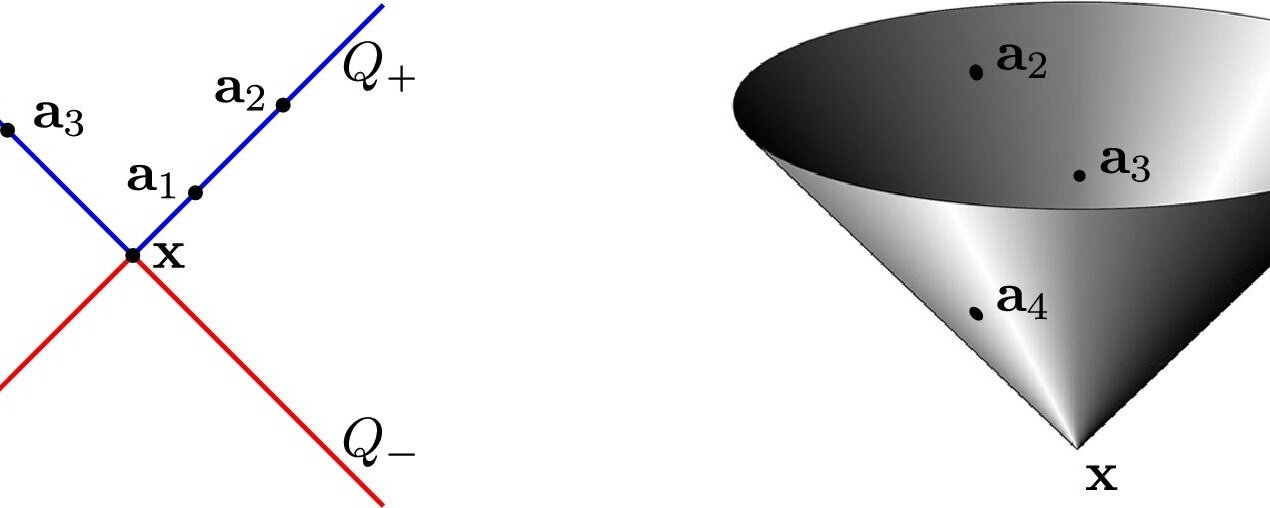
The summer holidays are ending, which for many concludes with a long drive home and reliance on GPS devices to get safely home. But every now and then, GPS devices can suggest strange directions or get briefly confused about your location. But until now, no one knew for sure when the satellites were in a good enough position for the GPS system to give reliable direction.

Measurement in quantum mechanics presents unique challenges. Observing one particle in an entangled pair determines the states of both, leading to critical inquiries: What constitutes a ‘measurement,’ and how does it influence our understanding of reality?

The complex mathematics underpinning quantum mechanics — incorporating concepts like Hilbert spaces, wave functions, and operators — can be intimidating, rendering entanglement less accessible to many.

Simply put, quantum entanglement is just too complicated for most people to fully understand. It defies classical intuitions, involves sophisticated mathematics, and urges us to reevaluate our understanding of reality.

Our universe is defined by the way it moves, and one way to describe the history of science is through our increasing awareness of the restlessness of the cosmos.

For millennia the brightest scientific minds in Europe and the Middle East believed that the Earth was perfectly still and that the heavens revolved around it, with a series of nested crystal spheres carrying each of the heavenly objects. Those early astronomers busied themselves with attempts to explain and predict the motion of those objects – the Sun, the Moon, each of the known planets, and the stars. Those predictions were excellent, and their systems able to explain the data well into the 16^th century.

Continue reading “The Universe is on the Move” »

The rise of the smaller models.

Mathematicians at Loughborough University have turned their attention to a fascinating observation that has intrigued scientists and cocktail enthusiasts alike: the mysterious way ouzo, a popular anise-flavored liquor, turns cloudy when water is added.

The Standard Model of particle physics is the mathematical description of the fundamental constituents and interactions of matter. While it is the accepted theory encapsulating our current state-of-the-art knowledge in particle physics, it is incomplete as it is unable to describe many glaring phenomena in nature.

Crivellin and Mellado’s article describes deviations in the decay of multi-lepton particles in the LHC, compared to how they should behave according to the Standard Model. These deviations, or anomalies, constitute excesses in the production of particles called electrons and its heavy cousin, the muon, on top of the predictions from the Standard Model.

“An anomaly is something that stands out as unusual or different from what is normal or expected. In this case, this is a deviation from the Standard Model of Particle physics. Anomalies can be important because they often signal that something unexpected or significant has happened,” says Crivellin.

For decades, extremal black holes were considered mathematically impossible. A new proof reveals otherwise.

A new theory suggests time travel might be possible without creating paradoxes.

TL;DR:

A physics student from the University of Queensland, Germain Tobar, has developed a groundbreaking theory that could make time travel possible without creating paradoxes. Tobar’s calculations suggest that space-time can adjust itself to avoid inconsistencies, meaning that even if a time traveler were to change the past, the universe would correct itself to prevent any disruptions to the timeline. This theory offers a new perspective on time loops and free will, aligning with Einstein’s predictions. While the math is sound, actual time travel remains a distant possibility.

“This is going to be the fastest AI computer ever launched to space,” Yanni Barghouty, CSC’s cofounder and CEO, told Space.com. “The goal of this mission is simply to demonstrate the successful operation of an AI-capable Nvidia GPU on orbit with minimal to no errors while operating.”

The GPU will fly aboard a cubesat built by San Francisco-based company Aethero, a maker of high-performance, space-rated computers. The GPU’s only task during its four-month orbital mission will be to make mathematical calculations, the results of which will be beamed to Earth and carefully checked.