A small community of mathematicians is using a software program called Lean to build a new digital repository. They hope it represents the future of their field.
Category: mathematics – Page 103
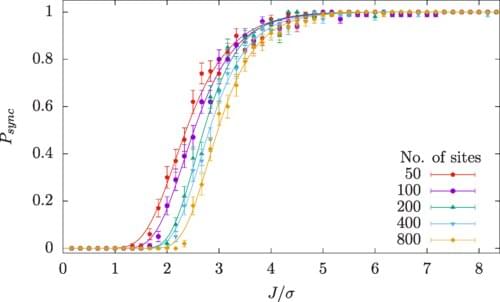
Physicists from Trinity have unlocked the secret that explains how large groups of individual “oscillators”—from flashing fireflies to cheering crowds, and from ticking clocks to clicking metronomes—tend to synchronize when in each other’s company.
Their work, just published in the journal Physical Review Research, provides a mathematical basis for a phenomenon that has perplexed millions—their newly developed equations help explain how individual randomness seen in the natural world and in electrical and computer systems can give rise to synchronization.
We have long known that when one clock runs slightly faster than another, physically connecting them can make them tick in time. But making a large assembly of clocks synchronize in this way was thought to be much more difficult—or even impossible, if there are too many of them.
Strategy accelerates the best algorithmic solvers for large sets of cities.
Waiting for a holiday package to be delivered? There’s a tricky math problem that needs to be solved before the delivery truck pulls up to your door, and MIT researchers have a strategy that could speed up the solution.
The approach applies to vehicle routing problems such as last-mile delivery, where the goal is to deliver goods from a central depot to multiple cities while keeping travel costs down. While there are algorithms designed to solve this problem for a few hundred cities, these solutions become too slow when applied to a larger set of cities.
The solver algorithms work by breaking up the problem of delivery into smaller subproblems to solve — say, 200 subproblems for routing vehicles between 2,000 cities. Wu and her colleagues augment this process with a new machine-learning algorithm that identifies the most useful subproblems to solve, instead of solving all the subproblems, to increase the quality of the solution while using orders of magnitude less compute.
Their approach, which they call “learning-to-delegate,” can be used across a variety of solvers and a variety of similar problems, including scheduling and pathfinding for warehouse robots, the researchers say.
More than a score of companies are pushing to be early winners in the race for self-driving taxis — robotaxis — with the potential that brings to capture the entire value chain of car transport from your riders. They are all at different stages, and they almost all want to convince the public and investors that they are far along.
To really know how far along a project is, you need the chance to look inside it. To see the data only insiders see on just how well their vehicle is performing, as well as what it can and can’t do. Most teams want to keep those inside details secret, though in time they will need to reveal them to convince the public, and eventually regulators that they are ready to deploy.
Because they keep them secret, those of us looking in from the outside can only scrape for clues. The biggest clues come when they reach certain milestones, and when they take risks which tell us their own internal math has said it’s OK to take that risk. Most teams announce successes and release videos of drives, but these offer us only limited information because they can be cherry picked. The best indicators are what they do, not what they say.
Working with two teams of mathematicians, DeepMind engineered an algorithm that can look across different mathematical fields and spot connections that previously escaped the human mind. The AI doesn’t do all the work—when fed sufficient data, it finds patterns. These patterns are then passed on to human mathematicians to guide their intuition and creativity towards new laws of nature.
“I was not expecting to have some of my preconceptions turned on their head,” said Dr. Marc Lackenby at the University of Oxford, one of the scientists collaborating with DeepMind, to Nature, where the study was published.
The AI comes just a few months after DeepMind’s previous triumph in solving a 50-year-old challenge in biology. This is different. For the first time, machine learning is aiming at the core of mathematics—a science for spotting patterns that eventually leads to formally-proven ideas, or theorems, about how our world works. It also emphasized collaboration between machine and man in bridging observations to working theorems.
Computer simulations and visualizations of knots and other objects have long helped mathematicians to look for patterns and develop their intuition, says Jeffrey Weeks, a mathematician based in Canton, New York, who has pioneered some of those techniques since the 1980s. But, he adds, “Getting the computer to seek out patterns takes the research process to a qualitatively different level.”
The authors say the approach, described in a paper in the 2 December issue of Nature1, could benefit other areas of maths that involve large data sets.
We can add suggesting and proving mathematical theorems to the long list of what artificial intelligence is capable of: Mathematicians and AI experts have teamed up to demonstrate how machine learning can open up new avenues to explore in the field.
While mathematicians have been using computers to discover patterns for decades, the increasing power of machine learning means that these networks can work through huge swathes of data and identify patterns that haven’t been spotted before.
In a newly published study, a research team used artificial intelligence systems developed by DeepMind, the same company that has been deploying AI to solve tricky biology problems and improve the accuracy of weather forecasts, to unknot some long-standing math problems.
Graphene consists of a planar structure, with carbon atoms connected in a hexagonal shape that resembles a beehive. When graphene is reduced to several nanometers (nm) in size, it becomes a graphene quantum dot that exhibits fluorescent and semiconductor properties. Graphene quantum dots can be used in various applications as a novel material, including display screens, solar cells, secondary batteries, bioimaging, lighting, photocatalysis, and sensors. Interest in graphene quantum dots is growing, because recent research has demonstrated that controlling the proportion of heteroatoms (such as nitrogen, sulfur, and phosphorous) within the carbon structures of certain materials enhances their optical, electrical, and catalytic properties.
For the first time, computer scientists and mathematicians have used artificial intelligence to help prove or suggest new mathematical theorems in the complex fields of knot theory and representation theory.
The astonishing results have been published today in the pre-eminent scientific journal, Nature.
Professor Geordie Williamson is Director of the University of Sydney Mathematical Research Institute and one of the world’s foremost mathematicians. As a co-author of the paper, he applied the power of Deep Mind’s AI processes to explore conjectures in his field of speciality, representation theory.
Physics books of 2021
Posted in mathematics, particle physics
Explore 10 new works related to particle physics and astrophysics, plus a bonus book on math.