With a shrinking population and more than 10 million abandoned properties, the country is straining to match houses with curious buyers.

More than six months after the last update, Midjourney has released a new image model — but it’s a smaller jump.

Ad.

Midjourney CEO David Holz announced version 6.1 of the company’s image model via Discord. This new version builds on V6, released in late December, and promises more coherent, detailed, and visually appealing results.

Comparing color qualia structures through a novel similarity task in young children versus adults https://osf.io/preprints/psyarxiv/wdcu7Moriguchi, Y., Watana…

Visual riddles a commonsense and world knowledge challenge for large vision and language models.

Visual Riddles.

A commonsense and world knowledge challenge for large vision and language models.

Imagine observing someone scratching their arm; to understand why, additional context would be necessary.

---

Non-personalized content and ads are influenced by things like the content you’re currently viewing and your location (ad serving is based on general location). Personalized content and ads can also include things like video recommendations, a customized YouTube homepage, and tailored ads based on past activity, like the videos you watch and the things you search for on YouTube. We also use cookies and data to tailor the experience to be age-appropriate, if relevant.

Select “More options” to see additional information, including details about managing your privacy settings. You can also visit g.co/privacytools at any time.

Guy Burckhardt finds himself trapped in a perplexing and eerie reality, waking up to the same day, June 15th, over and over again. The world around him seems laced with an uncanny artificiality, and bizarre, aggressive advertisements abound. Desperate to escape this mysterious loop, Guy embarks on a tense journey to uncover the truth, only to stumble upon a shocking revelation about his existence and the world he inhabits. Frederik Pohl’s tale is a labyrinthine enigma, a suspenseful exploration of reality, manipulation, and the clandestine machinations of unseen forces.

Join this channel to get access to perks:
/ @thedarkcosmos1

Sign up for future TDC updates:
https://forms.gle/aw8WhM8c9EsR6HjQ8

🏆 CREDITS

Crude oil pipelines connecting the busiest Texas oil fields to a critical export hub across the state are nearly out of space, threatening to cap US oil exports at a time when the world needs more.

We consider an infinite series, due to Ramanujan, which converges to a simple expression involving the natural logarithm. We show that Ramanujan’s series represents a completely monotone function, and explore some of its consequences, including a non-trivial family of inequalities satisfied by the natural logarithm, some formulas for the Euler–Mascheroni constant, and a recurrence satisfied by the Bernoulli numbers. We also provide a one-parameter generalization of Ramanujan’s series, which includes as a special case another related infinite series evaluation due to Ramanujan.

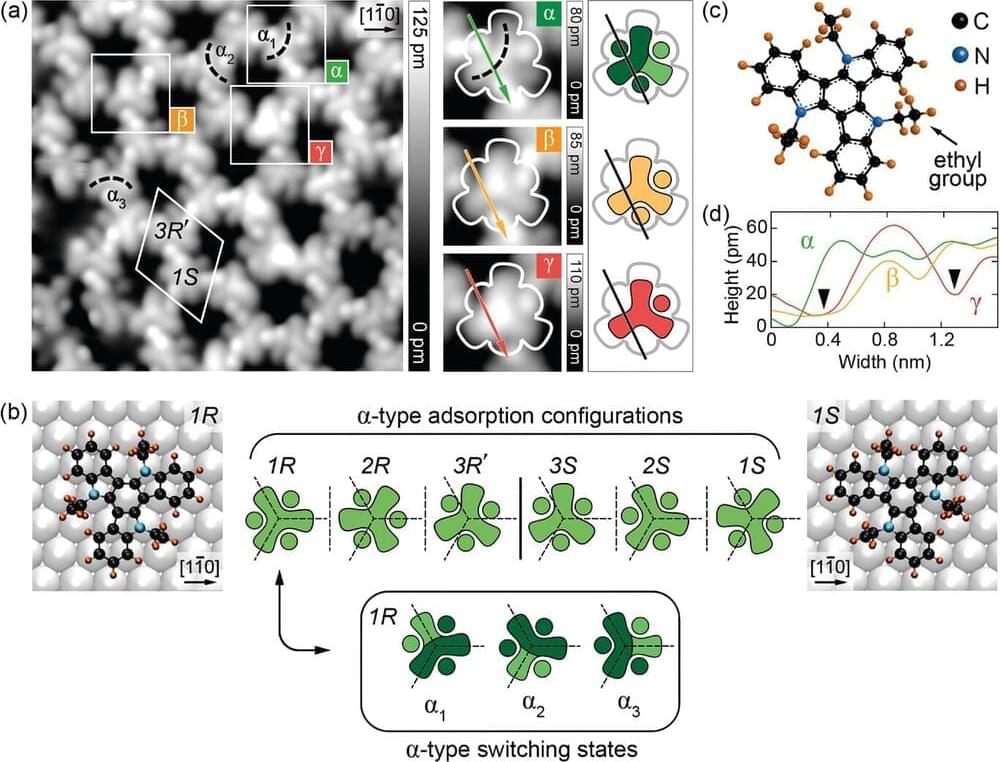
Researchers create a 2D array of molecular switches with 12 controllable states per molecule, showing promise for next-generation ultra-high-density memory systems.