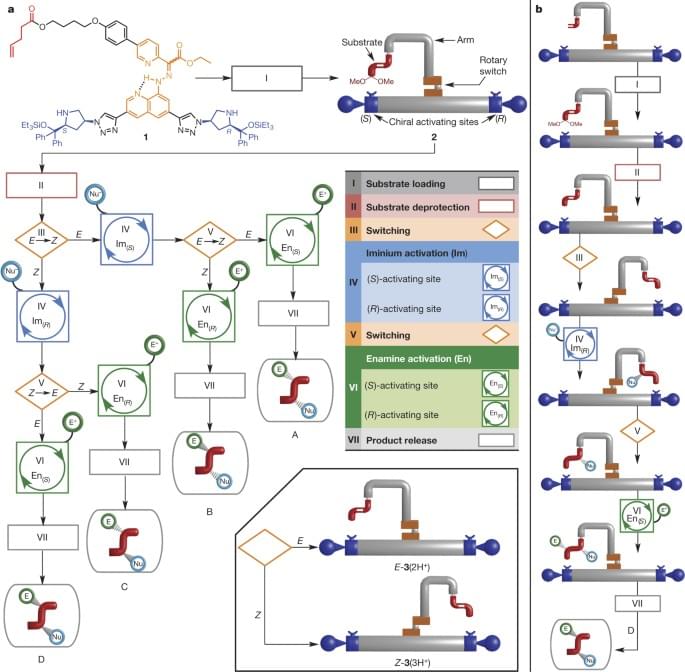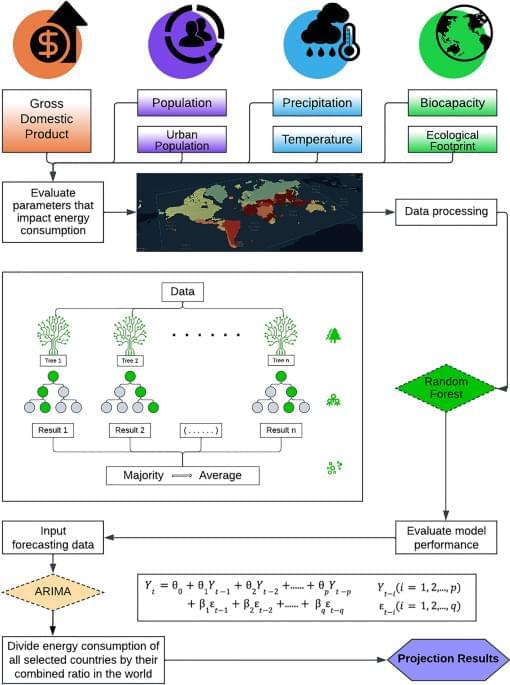
Throughout the history of human civilization, energy has been holding an imperative role in humanity’s progress1. Especially in the past few centuries, innovations in the harnessing of power have catalyzed humanity’s rapid growth2. Energy remains a key driver of human development3, with each revolution in industry and agriculture highlighting human’s reliance on it. Revolution in the eighteenth century was a turning point. The development of steam engines powered by fossil fuels led to significant technological progress4. Electricity has then opened new possibilities for the future5. Humanity has grown at a compound annual rate of 2.43% from 1965 to 2020, demonstrating our continued increasing demand for and consumption of energy6,7. However, the pace at which human being can progress as a civilization in the future remains uncertain.
While mankind was establishing its identity in the universe, insatiable human curiosity over the realm of civilization peaked in the 1960s8, which led to deeper cogitation of the concept of civilization. Providing that some of the extraterrestrial civilizations are highly likely million years more advanced than mankind, Soviet astrophysicist Nikolai Kardashev proposed a scale to classifies a civilization’s technological development based on its energy consumption9, which was later known as the Kardashev Scale. The scale initially categorized civilizations into three types. Type 1 is known as the planetary civilization, which features the capability of harnessing and utilizing all forms of energies that can be reached on the host planet, such as wind, solar, and geothermal power; Type 2 and 3, known as the stellar and galactic civilizations, respectively, are capable of extracting and utilizing all energy created by their respective systems9. Yet, such a scale proved lackluster in the quantitative presentation of the civilization types. Subsequently, Carl Sagan furthered the Kardashev Scale with data extrapolation, and proposed a continuous function quantifying the Kardashev Scale in index K10
$$K=\frac{.